النتائج 646 إلى 660 من 932
الموضوع: ديناميكية تحقيق القدر
- 22-07-2010, 09:59 PM #646
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
السلام عليكم اخوي العزيز فواز
وصلت لطريقة من خلال الاكسل نستطيع من خلالها جمع القيم السالبة المتتالية والموجبة المتتالية التي اخذتها مسبقا من التك تشارت
الان هذي البيانات المعدلة هي الشيئ الرئيسي لرسم شارت النبضات
الطريقة من خيار data نذهب الى خيار اسمة subtotals ويقوم بجمع القيم المتتالية والمتشابهة
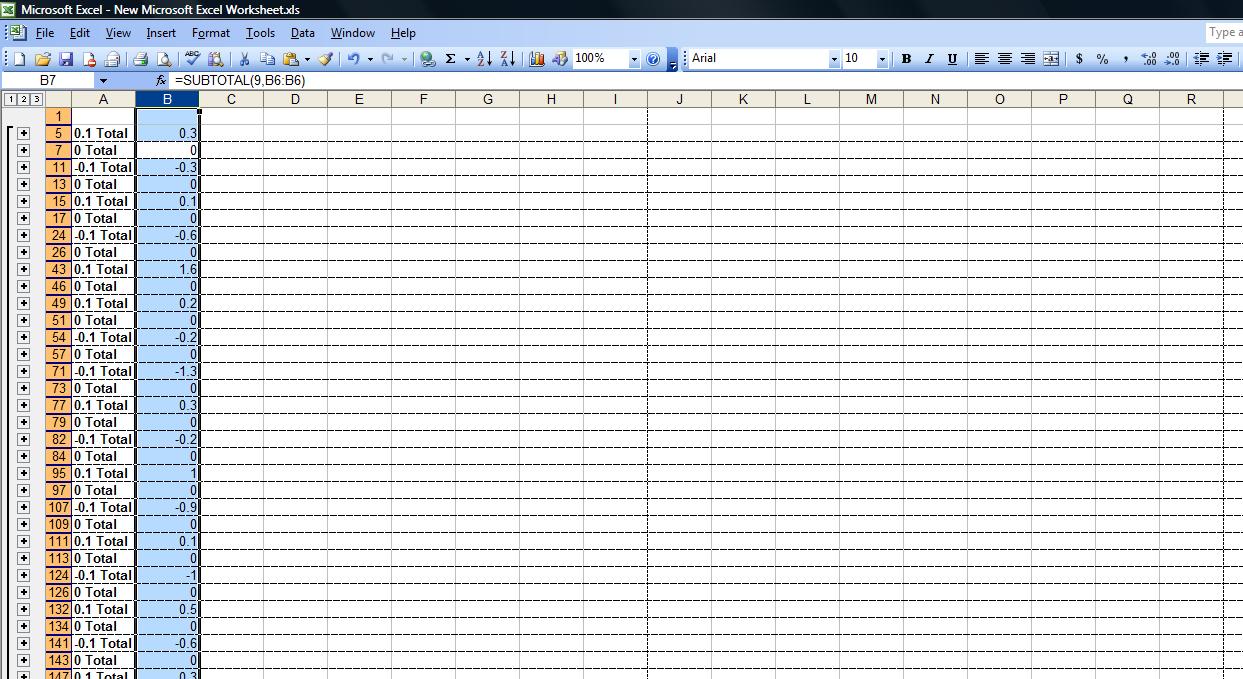
من ثم نعمل فلترة للقيم لحذف الاصفار من خلال
data------> filter------->advanced filter
وهكذا اصبحت القيم جاهزة لكن تبقى رسمها على تشارت النبضات
- 22-07-2010, 10:03 PM #647
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
- 22-07-2010, 10:39 PM #648
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
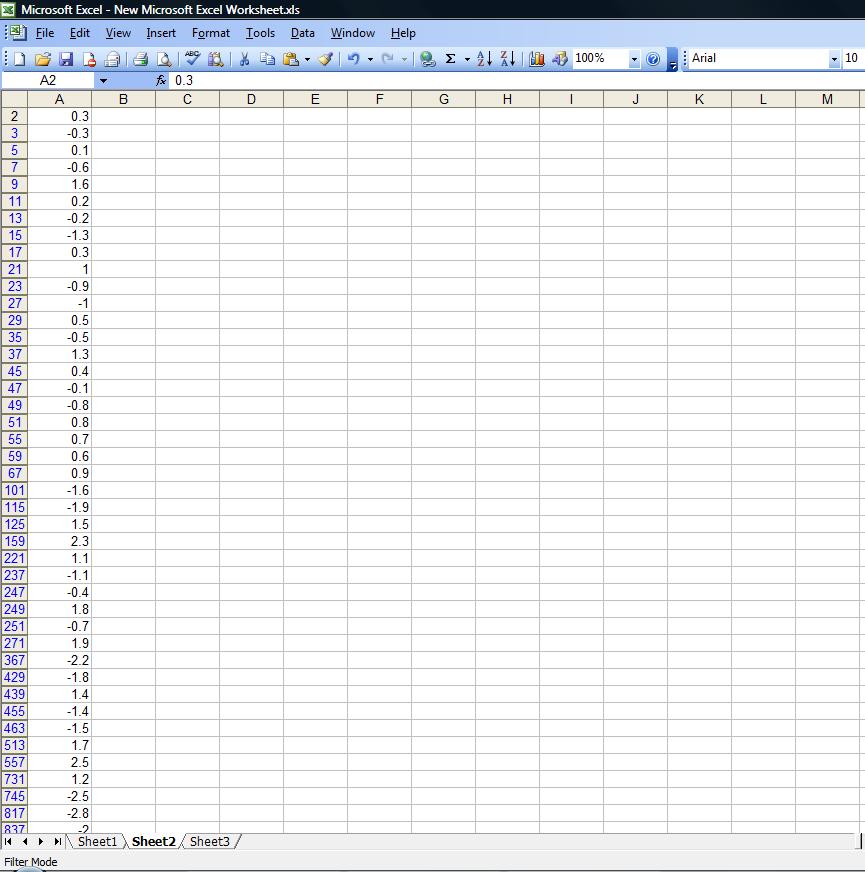
الظاهر انه عملية الفلترة فيها بعض المشاكل
- 23-07-2010, 12:23 AM #649
- 23-07-2010, 02:38 AM #650
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
اخى ماركوف اشكرك على سرعة الرد اولاً
ثانياً لم اقصد استخدام البرنامج لوظيفته الاساسية وهى عمل الشبكات العصبية باستخدام مدخلات معينة والحصول على محرجات تتنبأ بحركة السعر ولكن امكانيات البرنامج اكثر من ذلك لعمل المؤشرات واستخدامه لجميع المعادلات الرياضية والمنطقية والشرطيه وحساب المثثات ومتسلسلات فورير واساسيات حركة السعر ....... الخ بالاضافة الى ربط البرنامج مع الميتا تريدر والحصول مباشرة على شارت التكات وتصدير البيانات الى ملف الاكسل سواء للاسعار او اى عمليات قمت بها
برجاء الاهتمام بالبرنامج لانه بالفعل مفتاح الحل ان شاء الله علشان نوفر مجهود كبير
- 23-07-2010, 03:39 AM #651
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
This document gives a brief description of tachyon theory, and explains why tachyons cannot be used for faster-than-light communication.
Notes
This document is a qualitative, not quantitative, treatment of tachyon theory. To keep the mathematics simple and the diagrams comprehendible, the speed of light is assumed to be 1 space-unit per time-unit, and space is assumed to be one-dimensional.
The momentum–energy graph

The graph shows momentum (p) on the x-axis and energy (E) on the y-axis. The two yellow lines show the ‘light cone’ (in four dimensional space-time this would be a ‘hypercone’) — that is, where E = ± p. The region above and below the two lines is known as ‘timelike’, and the region to the left and the right is known as ‘spacelike’.
The standard particles

One of the famous equations of relativity states that E2 = m2c4 + p2c2. We are using units such that c = 1, so the equation becomes E2 = m2 + p2.
The solutions of this are the blue hyperbolae shown on the graph. Note that the hyperbolae cross the E-axis at E = m, consistent with E = m c2 when c = 1.
Particles on the upper branch are known as tardyons or bradyons (= “slow particles”) and they travel at subluminal speed. These include protons, neutrons and electrons. Particles with no mass move on the light cone, at the speed of light, and are known as luxons (= “light particles”). These include photons. Particles on the lower branch have negative mass, and these are the theorised ‘virtual particles’.
Tachyons

Another famous relativistic equation is E = m(1 - (v/c)2)-½. As tachyons, the theorised faster-than-light particles, have v > c, the square root is of a negative number and therefore is imaginary. But energy can’t be imaginary, so this tells us that the mass, m, is also imaginary and E is negative.
E2 = m2 + p2 becomes p2 - E2 = M2, where M is real. The solutions to this equation are the hyperbolæ in the spacelike region of the graph. As E < 0 for a tachyon, the pink portion represents tachyons.
From the graph we can see an interesting property of tachyons - as they lose energy (E becomes more negative) their momentum increases, unlike ordinary particles.
Electrically charged tachyons
If tachyons were electrically charged, as they travel faster than light they must produce Cherenkov radiation, lowering their energy and causing them to accelerate. Charged tachyons would therefore lead to a runaway reaction releasing an unlimited amount of energy. But as tachyon–antitachyon pairs would form spontaneously in a vacuum, the runaway reaction would lead to an unstable vacuum, so we must assume tachyons are uncharged.
Tachyon communication
Let’s look at the relativistic quantum mechanics of tachyons, discussing only spin-free tachyons in two-dimensional space-time for simplicity. These results still hold for other situations, but the mathematics is beyond the scope of this document. The wave function for a spin-free tachyon would satisfy the Klein–Gordon equation ((d/dt)2 + (d/dx)2 + m2) Φ = 0.
Any solution to this equation is a linear combination of solutions of the form Φ(t,x) = e-iEt + ipx. When m2 is negative (as with tachyons), we get two types of solution. If |p| >= |E| the solutions look like waves propagating faster than light. If |p| < |E| the solutions look like waves amplifying exponentially over time. We can now decide whether to consider the second type of solution.
If |p| < |E|
If we do consider the second type of solution, the Klein–Gordon equation can be solved for any reasonable initial data. We can prove that if Φ and dΦ/dt are zero outside some interval [-L,L] when t=0, they will be zero outside the interval [-L-|t|,L+|t|] at any time t. So localised disturbances do not propagate faster than light.
If |p| >= |E|
If we do not consider the second type of solution, the Klein–Gordon equation can only be solved for initial data whose Fourier transformations vanish in [-|m|,|m|]. The Paley–Wiener theorem tells us we cannot solve the equation for initial data that vanish outside some interval [-L,L]. This means we cannot localise the wave.
The final word on tachyon communication
To send a message faster than light using tachyons, we would have to encode the message on a localised tachyon field, and then send it off at superluminal speed. But this is impossible as local tachyon disturbances are subluminal, and superluminal tachyon disturbances cannot be localised.:
- 23-07-2010, 04:45 PM #652
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
السلام عليكم
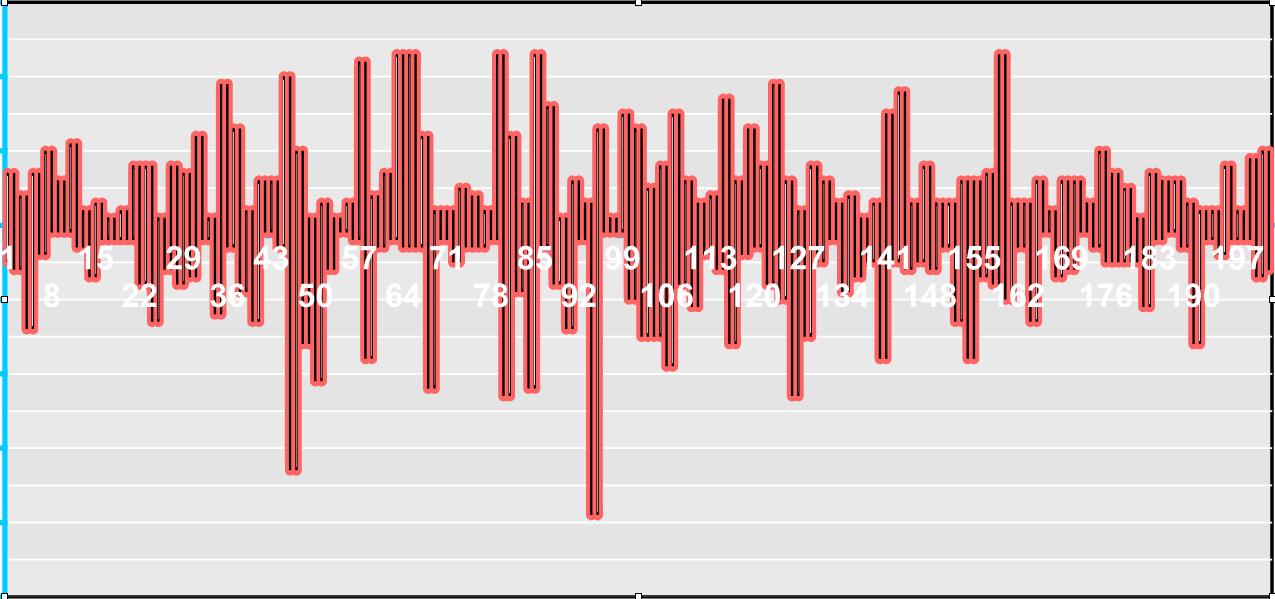
اخي فواز بعد عناء وصلت لهذا الشارت المرفق من خلال الاكسل وبرنامج اخر لرسم الشارت
ارجو ان يكون هو الشارت المطلوب
وهو لليورو دولار Pulse chart
هل هذا بالضبط هو المطلوب
- 23-07-2010, 11:00 PM #653
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
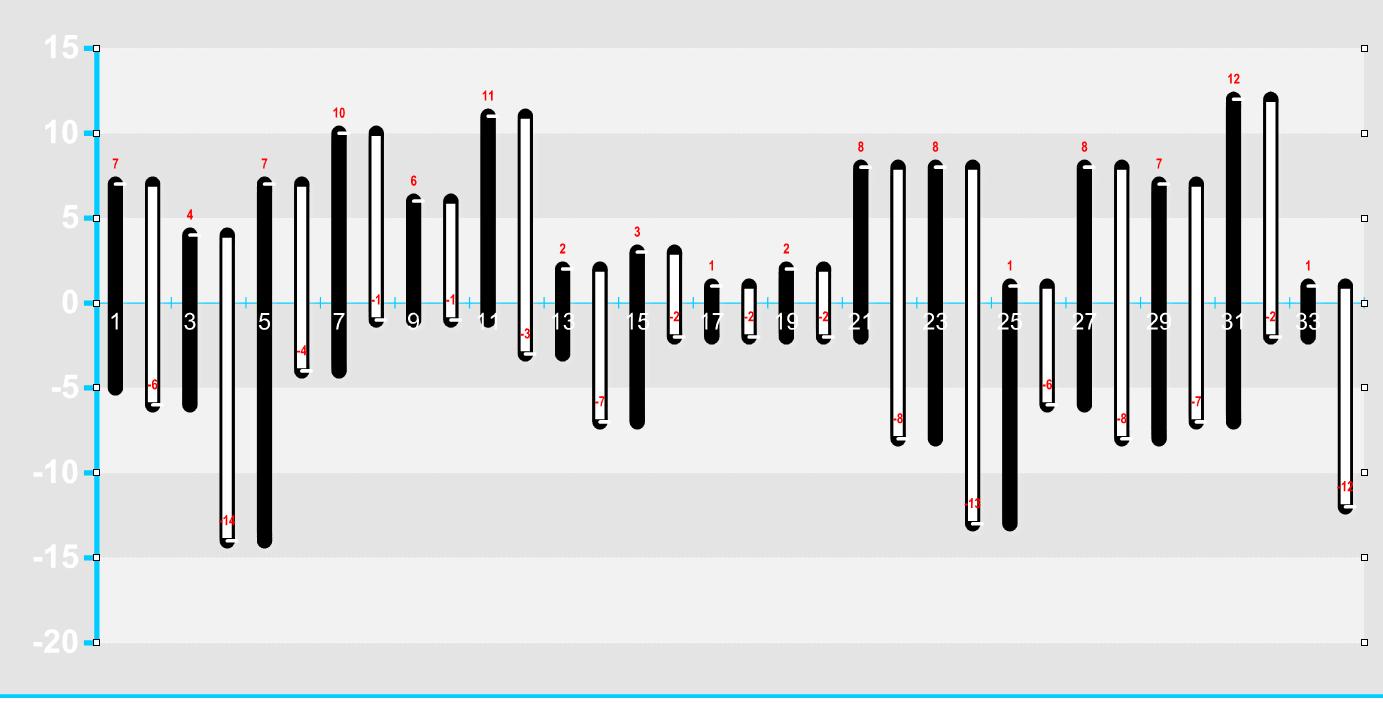
هذا شارت اوضح من السابق وكل نبضة مرقمة بالتسلسل
بعد تعديل البيانات بالاكسل تم رسم الشارت ببرنامج اسمة Swiff Char
- 24-07-2010, 09:51 AM #654
- 24-07-2010, 02:18 PM #655
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
إخواني الكرام
تفضّل أخوانا الغالي المهندس وضاح عطّار مشكوراً بعمل المطلوب
وهو شارت النبضات (بالصورة التي أراها أنا) والتي أوضحتها لكم في هذا الموضوع
لكن ليس شرطاً، أن تكون الصورة كذلك، فكل واحد له وجهة نظر مختلفة....والمجال واسع جداً للتطوير والإبداع
----------------------------
الخطوات كانت كالتالي:
1- عمل بريمج صغير يتم وضعه في الميتاتريدر ليسحب البيانات اللحظية ويسجلها على ملف CSV خارجي
هذا البريمج يقوم بعمل ملفان اثنان: واحد للتكات، وواحد للنبضات
2- فتح الملف بالإكسل ورؤية النبضات بشكل أرقام، ومن ثم تحويلها عبر أمر ماكرو الى أي شكل تريدونآخر تعديل بواسطة فواز الفوركس ، 24-07-2010 الساعة 02:26 PM
- 24-07-2010, 02:22 PM #656
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
هذا أحد أشكال شارت النبضات
وهو بشكل متذبذب ومتناوب حول محور أفقي
- 24-07-2010, 02:25 PM #657
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
وهذا هو الشكل الثاني له
وهو بشكل تراكمي
ونستطيع أن نطلق عليه اسم شارت، ويشبه الى حد كبير طريقة أخونا Oiltradeing
- 24-07-2010, 07:23 PM #658
 رد: ديناميكية تحقيق القدر
رد: ديناميكية تحقيق القدر
السلام عليكم و رحمة الله و بركاتة
شكرا للاخ فواز و الاخ وضاح لمساعدتهم المستمرة لاخوانهم, جعلها الله صدقة جارية و فى ميزان حسناتهم.
اذا امكن من الاخ فواز شرح طريقة عمل البريمج و الخطوات الاخرى بالتفصيل ان امكن.
تحياتى
- 24-07-2010, 09:58 PM #659
- 24-07-2010, 10:36 PM #660



 الأكثر زيارة
الأكثر زيارة