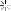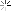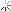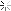العلاقه بين السعر والزمن لمعرفه الاتجاه

[aLcOmAnDa]

ياعزائي الوزن يختلف عن الكتله لان الكتله هي التعبير لثقل الاشياء مثلا وزن هذه السياره 2000 kg لاتقال وزنها بل يقال كتلتها يجب تصحيح المفاهيم لابد من ذلك

بالنسبة للي عاوز يحسب الوزن من الكتلة مع انى مش فاهم ازاى دا ممكن يتعمل على الشموع

يتم تطبيق المعادلة التالية

الوزن = الكتلة × تسارع الجاذبية

مع العلم ان تسارع الجاذبية = 9.81 متر/ثانية تربيع

[markov]

سؤال للأستاذ ماركوف


عل طريقتط في المتاجرة تعتمد قي اساسها على
Thermoeconomics

الطاقه هي قيمه فيزيائيه محدده .
اما الشعاع فهو قيمه فيزيائيه محدده ولكن له اتجاه ايضا .. خلي بالك .
وان استطعت التفريق بين هذا وذاك .. سيكون الامر سهلا عليك في هذا العالم البراق .
تحياتي .

[omri_fadwah_lakk]

In all the following interactive demonstrations, the following principles are used in the programming:
The seeds are given numbers from 1 up as far as you want to go.

The position of a seed s given in polar coordinates which involve two numbers:
a distance, r, measured from a fixed point called the origin and
an angle of rotation, theta, measured from a fixed direction called the axis
We use this system in everyday language when we say:
Look out! There's the teacher: 30 metres at 3 o'clock!
where the axis of 12 o'clock is straight ahead.

So we need a centre point or origin and a fixed line through it as an axis to measure the angles from.
A point is then uniquely identified by its distance r from the origin and its angle theta measured as a rotation about the origin from the axis.


The distance r of seed number s is √s,
so for example, seed number s = 9 is at a distance 3 from the origin
The angle theta that seed s has as seen from the origin is s × phi of a whole turn, where phi = 0.6180339... = (√5 – 1 ) / 2
so for example, seed s = 9 is 9 phi = 9 × 0.61804 = 5.5624 turns.
Since a whole turn takes us back to the starting direction, we can ignore the whole-number part and all we need is the fractional part 0.5624 of a turn but it does no harm to use 5.5624 either.

To plot the seedhead:
Most computer languages use a graphing system with x and y axes called cartesian coordinates.
They also provide functions on angles where the unit of angle is a radian that is, an angle is measured by the distance it makes around a circle of unit radius.
Because a unit circle has a circumference of 2π, there are 2π = 2 3.14159267... = 6.2831853... radians in one complete turn.
Now we can convert the distance-angle coordinates for a seed into cartesian coordinates as follows:
The x-coordinate is r cos( 2 π theta)
The y-coordinate is r sin( 2 π theta )
Here is a check on the values for the first 5 seeds:
s r theta x y
1 1 0.61803399 -0.7373689 -0.6754903
2 1.41421356 1.23606798 0.12363865 1.4087986
3 1.73205081 1.85410197 1.05384702 -1.3745568
4 2 2.47213595 -1.969427 0.3483639
5 2.23606798 3.09016994 1.8866942 1.20016041
Now plot your seeds on an x-y graph using the cartesian coordinates for each seed.
By multiplying the seed number by a different ratio to get its angle, you can experiment and see what seed heads would be like if nature used a different value for its turns-per-seed value too.

[omri_fadwah_lakk]

In all the following interactive demonstrations, the following principles are used in the programming:
The seeds are given numbers from 1 up as far as you want to go.

The position of a seed s given in polar coordinates which involve two numbers:
a distance, r, measured from a fixed point called the origin and
an angle of rotation, theta, measured from a fixed direction called the axis
We use this system in everyday language when we say:
Look out! There's the teacher: 30 metres at 3 o'clock!
where the axis of 12 o'clock is straight ahead.

So we need a centre point or origin and a fixed line through it as an axis to measure the angles from.
A point is then uniquely identified by its distance r from the origin and its angle theta measured as a rotation about the origin from the axis.


The distance r of seed number s is √s,
so for example, seed number s = 9 is at a distance 3 from the origin
The angle theta that seed s has as seen from the origin is s × phi of a whole turn, where phi = 0.6180339... = (√5 – 1 ) / 2
so for example, seed s = 9 is 9 phi = 9 × 0.61804 = 5.5624 turns.
Since a whole turn takes us back to the starting direction, we can ignore the whole-number part and all we need is the fractional part 0.5624 of a turn but it does no harm to use 5.5624 either.

To plot the seedhead:
Most computer languages use a graphing system with x and y axes called cartesian coordinates.
They also provide functions on angles where the unit of angle is a radian that is, an angle is measured by the distance it makes around a circle of unit radius.
Because a unit circle has a circumference of 2π, there are 2π = 2 3.14159267... = 6.2831853... radians in one complete turn.
Now we can convert the distance-angle coordinates for a seed into cartesian coordinates as follows:
The x-coordinate is r cos( 2 π theta)
The y-coordinate is r sin( 2 π theta )
Here is a check on the values for the first 5 seeds:
s r theta x y
1 1 0.61803399 -0.7373689 -0.6754903
2 1.41421356 1.23606798 0.12363865 1.4087986
3 1.73205081 1.85410197 1.05384702 -1.3745568
4 2 2.47213595 -1.969427 0.3483639
5 2.23606798 3.09016994 1.8866942 1.20016041
Now plot your seeds on an x-y graph using the cartesian coordinates for each seed.
By multiplying the seed number by a different ratio to get its angle, you can experiment and see what seed heads would be like if nature used a different value for its turns-per-seed value too.

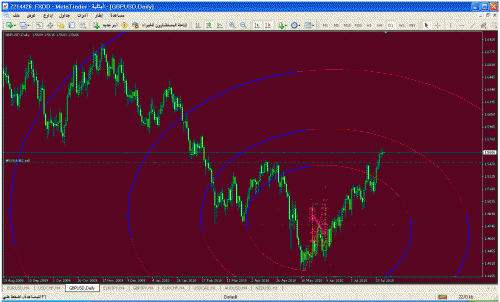
انا احاول اطبق الكلام اللى في الاقتباس على اي قمه اوقاع سعري



ولكن لم توضح الرويه عندي للان ( الفكره تقول عند القمه او القاع سوف تنكسرالاسعار بزاويه لو نفرض هذا الزاويه هي theta ولكن انا ماني عارف ارسمها على الشارت , بحيث نعتبر هذه الزاويه دعم او مقاومه للسعر) عسى اي واحد يساعدنا في تطوير هالفكره

[omri_fadwah_lakk]

Trigonometry Primer I



This tutorial is for Processing version 1.1+. If you see any errors or have comments, please let us know. This tutorials is from the book, Processing:Creative Coding and Computational Art, Ira Greenberg, Friends of ED 2007.


Trigonometry (really just a couple of the trig functions) is central to graphics programming. That being said if you're anything like me you probably have a hazy memory of trig. Perhaps you remember the mnemonic device soh-cah-toa, used to remember the relationships between the trig functions and a right triangle. Here's a diagram to awaken your memory.

• soh stands for "sine equals opposite over hypotenuse." "Opposite" refers to the side opposite the angle.
• cah stands for "cosine equals adjacent over hypotenuse." "Adjacent" is the side next to the angle.
• toa refers to "tangent equals opposite over adjacent."

You should also notice in the figure that tangent equals sine(θ) over cosine(θ). You may also remember that sine and cosine are similar when you graph them, both forming periodic waves. Only the cosine wave is shifted a bit (90° or pi/2) on the graph, which is technically called a phase shift. I fully realize that it is a difficult to deal with this stuff in the abstract. Fortunately, there is another model, the unit circle (shown below) used to visualize and study the trig functions.



The unit circle is a circle with a radius of 1 unit in length—hence its imaginative name. When you work with the unit circle, you don't use the regular and trusted Cartesian coordinate system; instead you use a polar coordinate system. The Cartesian system works great in a rectangular grid space, where a point can be located by a coordinate, such as (x, y). In a polar coordinate system, in contrast, location is specified by (r, θ), where r is the radius and θ (the Greek letter theta) is the angle of rotation. The unit circle has its origin at its center, and you measure angles of rotation beginning at the right-middle edge of the unit circle (facing 3 o'clock) and moving in a counterclockwise direction around it.

In the unit_circle diagram, the point p is at 45° or pi / 4. You can use pi also to measure around the unit circle, as illustrated in the figure. Halfway around the circle (180°) is equal to pi radians, and all the way around the circle is equal to 2pi radians and also 0 radians, since a circle is continuous and ends where it begins. The number pi is a constant that is equal to the circumference of a circle divided by its diameter, and is approximately 3.142.

In the polar system, you use radians to measure angles, instead of degrees. The angle of rotation in radians is commonly referred to as θ (the Greek letter theta). The arc length of this rotation is calculated by r*θ where r is the radius. In a unit circle, with a radius of 1, θ is equal to the arc length of rotation (arc s in unit circle diagram). It's nice to know the arc length, but most of the time (in computer graphics), you really just want to know the location of a point in relation to the unit circle. For example, if I wanted to rotate a point around the unit circle, I'd need to know how to place and move the point in a circle. With the unit circle, this is an incredibly easy task and precisely the kind of thing trig is used for.

There is a really simple relationship between the trig functions and the unit circle. Notice in the unit circle diagram that from point p on the ellipse, a right triangle is formed within the unit circle. This should immediately make you think of good old Pythagoras. Notice also that r (the radius) is the hypotenuse of the right triangle. In addition, you now also know that with the trig functions, you can use theta and any one side (opposite, adjacent, or hypotenuse) to solve the rest of the triangle. The big payoff of these relationships, for our purposes, is that to translate point p in the polar coordinate system to the Cartesian coordinate system (the system used by our monitors), you would use these simple expressions:

x = cosine(theta) * radius
y = sine(theta) * radius

These seemingly humble little expressions are very powerful and can be exploited for all sorts of expressive and organic purposes.

Here's how you actually use the trig functions in Processing:

float x = cos(radians(angle)) * radius;
float y = sin(radians(angle)) * radius;
Notice the function call (radians(angle)) inside each of the trig function calls. Remember that theta is measured in radians, in the polar coordinate system. However, in the Cartesian coordinate system, you work in degrees. To convert between radians and degrees and vice versa, you can use the following expressions:

theta = angle*pi/180
angle = theta*180/pi

Or better yet, just use Processing's handy conversion functions:

theta = radians(angle)
angle = degrees(theta)

Lastly, I include a Processing sketch that clearly demonstrates how the unit circle and sine function relate. A while back I came across a Java applet on the Web that showed this relationship (sorry, but I don't remember the link), and I thought it was helpful, so I created a version in Processing (screen-shot below): /**



نحن سوف نعتبر نقطه القمه او القاع هي origion point

[omri_fadwah_lakk]

وهذه دفعه من أسئلة علل
ثالثا: أسئلة علل
1- الفوتون لايمكن تعجيلة ؟
Eلأنة موجات كهرومغناطيسية غيرمشحونة كما أنة ليس لة كتلة سكون ويسير بسرعة ثابتة هى سرعة الضوء
2- ليس للفوتون كتلة سكون ؟
Eلأن عند سكون الفوتون تفنى مادتة ويتلاشى كمادة ويتحول الى طاقة يمتصها الجسم الذى أوقف حركتة .
3- يقل الطول الموجى المصاحب لحركة الألكترون بزيادة سرعته ؟
Eمن معادلة دىبرولى l=h/mv فنلاحظ أن lµ1/v أى أن الطول الموجى يتناسب عكسيا مع السرعة فكلما زادت سرعة الألكترون قل الطول الموجى المصاحب لحركته0
4- للألكترون طبيعة مزدوجة ؟
Eلأنه جسم مشحون له كتلة وسرعة وكمية تحرك وتصاحب حركتة موجة l=h/p لذلك فله طبيعة مزدوجة .
5- ينتشر الصوت فى الهواء على هيئة امواج طولية فقط0
E بسبب ضعف قوى التماسك بين جزيئات الهواء وبعضها لدرجة اقل مما تتطلبه الموجة المستعرضة0
6- تتكون الأمواج الموقوفة فى الأوتار المشدودة المهتزة ؟
E عندما يهتز الوتر المشدود تحدث حركتين موجيتين إحداهما ساقطة والأخرى منعكسة وهما متفقين فى الطور ومتساويين فى التردد ولهما نفس السعة ومنتشرين فى اتجاهين متضادين فتتراكب الحركتان مكونة الموجة الموقوفة .
7- أقل تردد يصدره وتر مشدود يهتز هو تردد نغمته الأساسية 0
Eحيث أن ( n a n) ونظراً لأن الوتر يهتز كقطعة واحدة فى هذة الحالة فتكون (1= n) وهو أقل عدد من القطاعات لذا يكون تردد النغمة الأساسية هو أقل تردد



سوف نطبق الكلام ده على الاقتباس اللى فوق

[omri_fadwah_lakk]

ااعتقد ان وصلنا الى شى منطقي

[AL4EVER+AA]

اخواني ,,,, انتو تتكلمون عن العملات ؟
و الا عن ايش ؟

[omri_fadwah_lakk]

انظر يا صديقي .. عليك اولا ان تؤمن بان موجات الفوركس هي متساويه في الاصل ثم بعد ذلك عليك في التفكير باشياء قد يعتبرها البعض مجرد مضيعه للوقت .. مع انها لب الشغل كله .. هناك معاملين متغيرين اساسيين .. المعامل الاول المتغير اسمه معامل الانحسار والمعامل المتغير الثاني اسمه معامل التمدد .
هاذين المعاملين الرئيسيين هما المسببين الرئيسيين فيما نراه اليوم من عشوائيه منظمه غريبه تحدث على شارتات المضاربه التي نعمل عليها .
والى حين حل لغزهما كاملا سيظل الشارت للاسف غامضا تماما للكثيرين منٌا .
تحياتي .

في البصريات، قانون سنيل (بالإنجليزية: Snell's law‏)، (ويعرف أيضا بقانون سنيل - ديكارت)، هو صيغة رياضية تصف العلاقة ما بين زوايا الإنعكاس والإنكسار، عندما ينتقل الضوء أو غيره من الأمواج ما بين وسطين مختلفين، مثل الهواء والماء. وبموجب هذا القانون، تكون نسبة جيوب زوايا الإنعكاس أو الإنكسار قيمة ثابتة مرتبطة بطبيعة الوسط الذي تعبره الأمواج. ينطبق هذا القانون على تنقل الأمواج في أوساط متجانسة ومتماثلة الخصائص في كل الإتجاهات.

يقوم قانون سنيل على مبدئين هما:

* توجد جميع الأمواج الساقطة والمنعكسة والمنكسرة على نفس السطح.
* إذا كانت θ1 هي زاوية سقوط الموجة على السطح الواصل بين الوسطين (1) و(2)، و θ2 هي زاوية إنكسار، وv2 وv1، هما سرعتا الموجة تباعا في الوسطين (1) و(2)، يكتب قانون سنيل كالآتي :

\frac{\sin\theta_1}{\sin\theta_2} = \frac{v_1}{v_2} = \frac{n_2}{n_1}

أو

n_1\sin\theta_1 = n_2\sin\theta_2\ حيث n1 وn2 معاملا الإنكسار تباعا في الوسطين (1) و(2).

إذا كان معامل إنكسار الوسط الأول أصغر من معامل إنكسار الوسط الثاني، أي أن سرعة الموجة في هذا الأخير تقل، مثل المرور من الهواء إلى الماء أو الزجاج، فإن زاوية الإنكسار تكون أقل من زاوية السقوط، والعكس بالعكس.

[Abdullah1985]

دمجتوا الفيزياء في الفوركس
والفلك
ويش بقى؟
لو فيه تشارت يوضح العلاقة بين سعر العملة وكميتها ونطبق عليها قوانين العرض والطلب ونوجد نقطة التوازن
وحتى يكون سهل نوجد الميل
انا مدري هل فيه حد اشتغل على السعر والكمية
وهل فيه تشارت يوضح سعر العملة وكميتها

[The.Demon]

دمجتوا الفيزياء في الفوركس
والفلك
ويش بقى؟
لو فيه تشارت يوضح العلاقة بين سعر العملة وكميتها ونطبق عليها قوانين العرض والطلب ونوجد نقطة التوازن
وحتى يكون سهل نوجد الميل
انا مدري هل فيه حد اشتغل على السعر والكمية
وهل فيه تشارت يوضح سعر العملة وكميتها

ممكن تشرح فكرتك اكثر وماذا ستستفيد من خط التوازن ؟