النتائج 1 إلى 15 من 103
الموضوع: النسبة الذهبية Phi φ
- 01-10-2013, 11:02 PM #1
 النسبة الذهبية Phi φ
إخوتي في الله
النسبة الذهبية Phi φ
إخوتي في الله
السلام عليكم ورحمة الله وبركاته
واسعد الله اوقاتكم بكل خير
أما بعد موضوعنا اليوم عن النسبة الذهبية والتي حيرت الكثير من علماء الرياضيات وهي عبارة عن الرقم Phi φ وهو عبارة عن جذر 5 + 1 ÷ 2 = 1.61803398875
ويرمز لهذا الرقم عند العامة ( 0.618 )
وبالنسبة لعلماء الرياضيات فأن هذا الرقم يمثل الصورة الجمالية للهندسة الكسرية ( Fractal Geometry) ومن اهم ما يميز الرقم φ هو النقطة التي يتواجد فيها φ دائما تكون نقطة مفصلية أي ان نقطة تواجد φ في الطبيعة تقتصر دائما على النقاط المفصلية
والتي تعرف بـ المفصل ودور هذا المفصل هو الربط بين الاجزاء في الطبيعة بما في ذلك جسم الانسان
ولتوضيح اكثر خذ هذا المثال
الركبة : هي ذلك النتوء الكبير في وسط رِجل الإنسان. الذي يفصل بين الساق والفخذ
أي ان الركبة هي نقطة تواجد φ وسط رِجل الإنسان وكذلك كل المفاصل الموجودة في جسم الانسان تمثل نقطة تمركز الرقم φ وكذلك الحال في النبات والحيوان وطبيعة بشكل عام .
اخواني دعونا نفكر بصوت عالي ما هي الاسباب الرياضية التي تجعل الرقم φ يختار هذه النقطة دون سواها إذا تمكنا من الاجابة على هذا السؤال حين اذن نستطيع التنبؤ بموقع تمركز φ
معنى ذلك انك تستطيع التنبؤ في بموقع تواجد النقطة φ لدى السلوك الجماعي بمعنى اخر يمكنك التنبؤ بنقطة التي يتمركز فيها φ والتي تمثل المفصل الذي يربط كل موجة بالأخرى
أخواني لن أطيل عليكم
بمشيئة الله سنقوم بشرح أهم الأسباب الرياضية التي تجعل الرقم φ يختار هذه النقطة دون سواها ولكن بعد هذا الفيديو
- 01-10-2013, 11:03 PM #2
 رد:النسبة الذهبية Phi φ
( س ) ما هي النسبة الذهبية ومن إين أتت
رد:النسبة الذهبية Phi φ
( س ) ما هي النسبة الذهبية ومن إين أتت
( ج ) النسبة الذهبية هي عبارة عن الرقم الذهبي وهو 1.618
( س ) من إين أتى هذا الرقم الذهبي
( ج ) أن الرقم الذهبي أو ما يعرف باسم النسبة الذهبية أتى من متوالية فيبوناتشي
( س )وما هي هذه المتوالية فيبوناتشي
( ج ) متتالية فيبوناتشي أو ما يعرف باسم Fibonaccinumbers
هي عبارة عن أرقام متتالية ذات سلسلة رقميه لا متناهية تبدأ هذه السلسلة من صفر إلى مالا نهاية
0 . 1 . 2 . 3 . 5 . 8 . 13 . 21 . 34 . 55 .89 . 144 . 233 . 377 . 610 . 987 ....
وهكذا إلى مالا نهاية
نقوم بجمع أول والثاني ليعطينا ناتج الرقم الثالث
ونجمع الثالث والثاني ليعطينا الرابع
ونجمع الرابع والثالث ليعطينا الخامس ونجمع
الخامس والرابع ليعطينا السادس وهكذا ونجمع
0 + 1= 1
1 + 1 = 2
1 + 2 =3
2 + 3 =5
3 + 5 =8
وهكذا
( س ) ما هي العلاقة بين هذه الأرقام و النسبه الذهبية
( ج ) الجواب بسيط أخي الفاضل إذا قمة قسمة أي عدد في المتتالية على الرقم الذي قبة سيكون الناتج هو 1.618
أي النسبة الذهبية
مثال
610 ÷ 377 = 1.618
377 ÷ 233 = 1.618
233 ÷ 144 = 1.618
144 ÷ 89 = 1.618
وهكذا عرفنا من أين أتت النسبة الذهبية
( س ) هل هناك نسب للفيبوناتشي غير النسبة الذهبية
( ج ) لا
( س ) كيف وإنا عندما استخدام الفيبو أجد نسبة 23.6 % و 38.2 % و 61.8 %
( ج ) أخي الفاضل مثل ما قسمنا أرقام المتتالية على الرقم الذي قبله لنوجد النسبة الذهبية
سنقوم الآن بقسمة النسب على بعضها البعض لنوجد النسبة الذهبية على سبيل المثال نقسم 100% على 61.8%
100 ÷ 61.8 = 1.618
لنكرر العملية مره أخرى نقسم 61.8 على 38.2
61.8 ÷ 38.2 = 1.618
لنكرر العملية مره أخرى نقسم 38.2 على 23.6
38.2 ÷ 23.6 = 1.618
أن المقصود أخي الفاضل في النسب التي تراها في أداة الفيبو ماهي ألا مستويات النسبة الذهبية بين كل نسبه وأخرى
- 01-10-2013, 11:07 PM #3
 رد:النسبة الذهبية Phi φ
( س ) هل من الممكن ايجاد متتالية غير متتالية فيبوناتشي
رد:النسبة الذهبية Phi φ
( س ) هل من الممكن ايجاد متتالية غير متتالية فيبوناتشي
بحيث يقترب ناتج قسمة كل رقم من ارقام المتتالية الجديدة على الذي قبله من 1.618 شيئا فشيئا .
( ج ) الجواب نعم
( س ) كيف يمكن الحصول على المتتالية الجديدة
( ج ) نقوم بجمع الرقم 1والرقم 3 ليعطينا الرقم 4
ونجمع الرقم 2 والرقم 5 ليعطينا الرقم 7
ونجمع الرقم 3 والرقم 8 ليعطينا الرقم 11
ونجمع الرقم 5 والرقم 13 ليعطينا الرقم 18
وهكذا نجمع بحيث تقفز رقم في كل مرة تجمع فيها
1 . 2 . 3 . 5 . 8 . 13 . 21 . 34 . 55 .89 . 144 . 233 . 377 . 610 . 987 ....
( س ) هل سنحصل على نفس النتيجة في حال قفزنا رقمين في كل مرة
بحيث نجمع الرقم 1مع 5 ليعطينا الرقم 6
والرقم 2 مع الرقم 8 ليعطينا الرقم 10
والرقم 3 مع الرقم 13 ليعطينا الرقم 16
والرقم 5 مع الرقم 21 ليعطينا الرقم 26
والرقم 8 مع الرقم 34 ليعطينا الرقم 42
( ج ) الجواب نعم
( س ) معنى هذا الكلام بإمكاني الحصول على اكثر من متتالية من خلال عدد القفزات
( ج ) الجواب نعم وهذا جدول توضيحي لبعض هذه المتتاليات
- 01-10-2013, 11:07 PM #4
 ( س ) هل تريد ان تقول ان النسب الموجودة في اداة الفيبو ( 23.6 % و 38.2 % و 61.8 % ) ليس لها أي أهمية
( س ) هل تريد ان تقول ان النسب الموجودة في اداة الفيبو ( 23.6 % و 38.2 % و 61.8 % ) ليس لها أي أهمية
( ج ) انا لم اقل ذلك بل على العكس ان نسب الفيبو مهمه جداً ولكن طريقة استخدام هذه النسب في الاسوق المالية لا يقبلها العقل وحتى المنطق الرياضي
( س ) ولكن اغلب الكتب التي تتحدث عن هذه النسب ( 23.6 % و 38.2 % و 61.8 % ) على اساس انها نسب تصحيحية
( ج ) كلام جميل ولكن السؤال المهم هو كيف استطيع معرفة نسبة التصحيح لأي موجة هل هي نسبة 23.6 % او نسبة 38.2 % او نسبة 61.8 % بمعنى اخر هل يوجد في هذه الكتب طريقة توضح لي ما هو السبب الرياضي في اختلاف نسب التصحيح بين كل موجة وأخرى
( س ) معنى كلامك انك تشكك في صحة المعلومات الموجودة في معظم هذه الكتب
( ج ) هل هذه الكتب والمراجع هي كتب منزلة من السماء بحيث لا يجوز التشكيك في صحتها هذا من ناحية ومن ناحية اخرى الببغاء يستطيع ترديد سياق الكلام ولكن هل يستطيع معرفة معنى الكلام كذلك الكثير من الناس يردد ما يسمع ولكن للأسف الشديد لا يعرف ما هو معنى الكلام الذي يردده فإذا كنت تريد ترديد الكلام مثل الببغاء فهذا شأنك وان كنت تريد الاحتكام للعقل والمنطق الرياضي اهلا وسهلا بكآخر تعديل بواسطة غالب بن الشيبه ، 01-10-2013 الساعة 11:11 PM
- 01-10-2013, 11:08 PM #5

- 01-10-2013, 11:09 PM #6
 تعريف ( φ ) مقياس الجمال
تعريف ( φ ) مقياس الجمال
هو عبارة عن هذا الرقم الثابت 1.61803398875
وعندما نستخدم لغة الرياضيات لكي نعبر عن مقياس جمال الصورة الموجودة في الطبيعة كل ما كانت مقاييس الصورة اقرب الى الرقم 1.61803398875 نلاحظ ان الصورة تبدو أكثر جمالاً وعندما تبتعد مقاييس الصورة عن الرقم 1.61803398875 تكون الصورة اقل جمالاً وجاذبية
وعلى سبيل المثال كلما كان مقاييس وجه المرأة اقرب الى الرقم 1.61803398875 كانت أكثر جمالاً وجاذبية وهذا معروف لدى اختصاصي التجميل وعندما تبتعد مقاييس وجه المرأة عن الرقم 1.61803398875 نقول ان هذه المرأة ليست جميلة
بمعنى اخر إذا كان مقاس وجه أمل = 89 ÷ 55 = 1.618181818181818
بينما مقاس وجه حنان = 55 ÷ 34 = 1.617647058823529
حين إذن نقول ان أمل تبدو أكثر جاذبية و جمال من حنان
ومعنى هذا الكلام ان طول الجزء العلوي من وجه الانسان تقسيم الجزء السفلي ليس بضرورة ان يكون الناتج = 1.618 ربما يكون 1.625 او ربما 1.6 او 1.64
معنى ذلك ان قيمة φ غير ثابته ممكن تكون 1.636 و ممكن تكون 1.618 وممكن 1.6 وهذا يعني ان قيمة φ متأرجحه وغير ثابته وكذلك الحال في الاسواق المالية ممكن يصحح السعر الى نسبة 61.8% او الى نسبة 65% وممكن يصحح الى نسبة 57.1% لكنها تكون دائما اقرب الى النسبة الذهبية وهذه النسب المختلفة هي في الاساس نتيجة قسمة احد ارقام المتتالية على الرقم الذي قبله مثل قسمة 13 ÷ 8 = 1.625 او قسمة 11 ÷ 7 = 1.571 وهذا يعني ان بإمكانك معرفة قيمة التصحيح من خلال نوع ورقم المتتاليةآخر تعديل بواسطة غالب بن الشيبه ، 01-10-2013 الساعة 11:12 PM
- 01-10-2013, 11:11 PM #7

ممتاز جدا متابع معك عمي غالب
جزاك الله كل خير
- 01-10-2013, 11:16 PM #8
 رد:النسبة الذهبية Phi φ
نشأت الهندسة الفركتلية fractal geometry في الستينات والسبعينات من القرن العشرين عن دراسات <B. ماندلبروت> في تعقيد الأشكال. وقد اشتق ماندلبروت كلمة فركتلي fractal من الكلمة اللاتينية fractus (ومعناها «مكسور») لتدل على الطبيعة المجزأة وغير النظامية لهذه الأشكال.
رد:النسبة الذهبية Phi φ
نشأت الهندسة الفركتلية fractal geometry في الستينات والسبعينات من القرن العشرين عن دراسات <B. ماندلبروت> في تعقيد الأشكال. وقد اشتق ماندلبروت كلمة فركتلي fractal من الكلمة اللاتينية fractus (ومعناها «مكسور») لتدل على الطبيعة المجزأة وغير النظامية لهذه الأشكال.
▪ تدل الفركتليات على التشابه الذاتي، وهذا يعني أن للشكل منظرا متماثلا عند أي تكبير. فأي جزء صغير من البنية يماثل الكل إلى حد كبير.
▪ يكون التشابه الذاتي دقيقًا أو إحصائيًا، فالشجرة الصنعية (سلسلة الصور في اليمين) تماثل تكرارا دقيقا للنموذج عند قيم تكبير مختلفة. أما بالنسبة إلى الشجرة الحقيقية (سلسلة الصور في اليسار) فإن الشكل لا يتكرر بشكل دقيق، ولكن عوضا عن ذلك فإن الخصائص الإحصائية لهذه النماذج هي التي تتكرر. إن معظم النماذج في الطبيعة تخضع للتشابه الذاتي الإحصائي،
▪ يمكن تمييز البنى الفر كتلية بدلالة «البعد» dimension أو التعقيد. فالبعد هو رقم غير صحيح كما هي الأبعاد المألوفة 1 و 2 و 3 في الهندسة الإقليدية. وعوضا عن ذلك فإن أبعاد البنى الفر كتلية هي أرقام فركتلية، على سبيل المثال، يكون بعد الخط الفر كتلي بين 1 و 2.

- 01-10-2013, 11:19 PM #9
 رد:النسبة الذهبية Phi φ
خلال الثمان سنوات خبرة في مجال النسبة الذهبية اكتشفت في الثلاث سنوات الأولى وكنت في هذه السنوات الثلاث اطبق كل ما هو موجود في الكتب تطبيق حرفي كما هو الحال لدى معظم الناس ولكن بدون جدوى وأدركت في ذلك الوقت ان العلم الحقيقي للنسبة الذهبية غير موجود في الكتب بمعنى أخر هو علم يقتصر على فئه معينة من الناس وغير متاح لعامة الناس
رد:النسبة الذهبية Phi φ
خلال الثمان سنوات خبرة في مجال النسبة الذهبية اكتشفت في الثلاث سنوات الأولى وكنت في هذه السنوات الثلاث اطبق كل ما هو موجود في الكتب تطبيق حرفي كما هو الحال لدى معظم الناس ولكن بدون جدوى وأدركت في ذلك الوقت ان العلم الحقيقي للنسبة الذهبية غير موجود في الكتب بمعنى أخر هو علم يقتصر على فئه معينة من الناس وغير متاح لعامة الناس
ومنذ عام 2008 توجهت الى الابحاث العلمية في مجال النسبة الذهبية ومازالت هذه الابحاث مستمرة الى الان واكتشفت خلال هذه الفترة ان علم النسبة الذهبية مرتبط بعلوم الطبيعة مثل علم الفيزياء وعلم الهندسة الكسرية ( Fractal Geometry)
ومنها على سبيل المثال قانون الانعكاس فصورة التي تتشكل على الشارت تنعكس في موقع اخر من الشارت ولكن بحجم مختلف كما هو الحال في الاشكال الموجودة في علم الهندسة الكسرية وهنا توقفت لكي اعيد مفهومي حول قوانين الفيزياء وعلم الهندسة الكسرية وخرجت بمفهوم جديد لحركة العشوائية او ما يسمى السلوك العشوائي وهذا المفهوم الجديد يتعارض مع بمفهوم الحركة العشوائية الذي يدرس في الجامعات الغربية ولكن تمكنت من اثبات وجهة نظري من الناحية الرياضية .
اليوم سأناقش معك مفهومي حول الحركة العشوائية في الاسواق المالية ويتمثل هذا المفهوم الجديد في ثلاث نقاط أساسية
1- 13 نموذج زمني للموجات الدافعة كل نموذج يختلف عن الاخر يقابله من ناحية اخرى 8 نماذج زمنية للموجات التصحيحية كل نموذج يختلف عن الاخر
2- 5 نموذج للموجات الدافعة السعرية كل نموذج يختلف عن الاخر يقابله من ناحية اخرى 3 نماذج للموجات التصحيحية السعرية كل نموذج يختلف عن الاخر
3- نظام التبادل ويمثل هذا النظام قانون التبادل الذي يسمح في تبادل الادوار بين نماذج الموجات السعرية ونموذج الموجات الزمنية بحيث يكون عدد نموذج الموجات السعرية الدافعة 13 نموذج بينما نموذج للموجات الدافعة الزمنية 5 نماذج
وكذلك الحال مع نماذج الموجات السعرية التصحيحية 8 نماذج سعرية تصحيحية يقابلها 3 نماذج للموجات التصحيحية الزمنية
وبعد هذه المقدمة سأقوم بمشيئة الله تعالى في الايام القادمة بشرح كل نقطة من النقاط الثلاثة
- 01-10-2013, 11:24 PM #10
 رد:النسبة الذهبية Phi φ
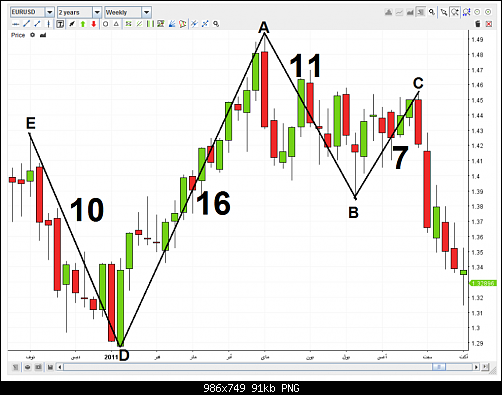
حديثنا اليوم هو عن احد النماذج التصحيحية للموجات الزمنية وهو النموذج الخارجي
رد:النسبة الذهبية Phi φ
حديثنا اليوم هو عن احد النماذج التصحيحية للموجات الزمنية وهو النموذج الخارجي
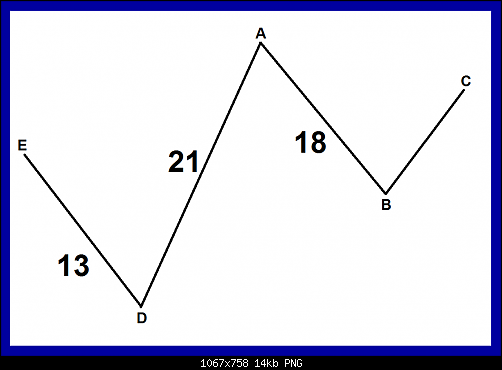
هناك قاعدة ثابته في هذا النموذج وهي ان الضلع BC اقصر من الضلع AB وكذلك الضلع ED اقصر من الضلع AD
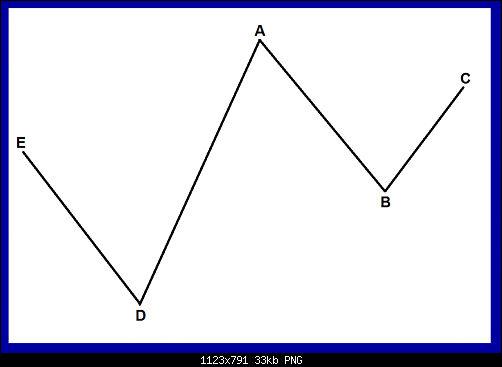
هذا من ناحية ومن ناحية اخرى إذا كان تقسيم الضلع ED على الضلع AD يساوي 38.2 فيبو يجب ان يكون تقسيم الضلع BC على الضلع AB يساوي 38.2 فيبو بمعنى اخر ان النسبة الناتجة من قسمة ED على AD ستكون هي نفس النسبة في حالة تقسيم الضلع BC على AB فإذا كان ED يساوي 61.8 من AD كذلك يجب ان يكون BC تقسيم AD يساوي 61.8 أي ان النسبة الموجودة في ED هي نفس النسبة الموجودة في BC
ويتم حساب هذه النسبة من خلال جدول المتتاليات الذهبية
- 01-10-2013, 11:26 PM #11
 رد:النسبة الذهبية Phi φ
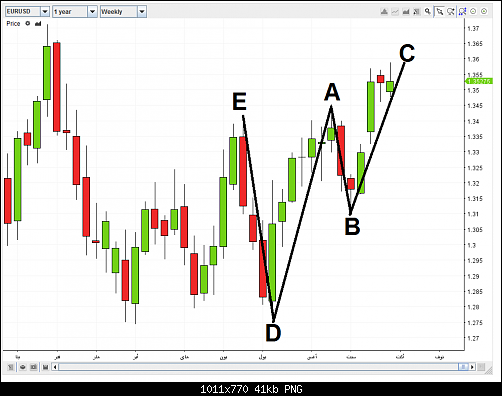
وقبل تطبيق هذا النموذج على الشارت ما رأيك ان نحاول ايجاد قيمة الضلع BC
رد:النسبة الذهبية Phi φ
وقبل تطبيق هذا النموذج على الشارت ما رأيك ان نحاول ايجاد قيمة الضلع BC
تخيل ان الضلع BC يمثل موجة تصحيحية صاعدة والسؤال الان هو متى تنتهي هذه الموجة الصاعدة
لدينا في هذا المثال الضلع ED عبارة عن 13 شمعة
والضلع AD عبارة عن 21 شمعة
والضلع AB عبارة عن 18 شمعة
فكم شمعة يجب ان تكون في الضلع BC
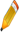
آخر تعديل بواسطة غالب بن الشيبه ، 01-10-2013 الساعة 11:56 PM
- 01-10-2013, 11:46 PM #12

قيمة الضلع 11 شمعة لكن اخي غالب انت تعتمد علئ بعد هندسي واحد حسابي ونحن في المتاجرة لدينا بعد زمني يجب وضعه في الحسبان وهو بعد يعتمد علئ البشر وبما ان الموضوع عشوائي ويحمل احتمالات فيمكن ان يحدث تفرع للشجرة في اي شكل احصائي اخر ثابت بعيد عن النسبة الذهبية او قريبا منها يعني يمكن ان يخرج الوجه قبيح او قبيح جدا او جميل او جميل جدا او حتئ مقبول
هل تعلم ان البنوك تعلم كل الاوامر ثم تدخل وتحرك السوق معك او عكسك حسب مصالحهم وهكذا تدرك حجم عامل الزمن او العامل الصعب حسابه عمليا لانه غيبي
تقبل خالص تحياتي
- 02-10-2013, 12:19 AM #13
 رد:النسبة الذهبية Phi φ
رد:النسبة الذهبية Phi φ
ممتاز 10 على 10 اخي عرابي الجواب هو 11 شمعة
اما بخصوص تدخل البنوك احب ان اقول لك ما انا الا شخص يحاول ان يبحث عن الحقيقة قد يصيب وقد يخطئ ولهذا السبب أرجو منك ان لا نستبق الاحداث خلينا نشوف ما هي الإيجابيات وسلبيات الفكرة
مع العلم ان لا يوجد شيء في هذا الكون كامل
الكمال لله وحده
- 02-10-2013, 12:23 AM #14
- 02-10-2013, 12:37 AM #15



 الأكثر زيارة
الأكثر زيارة
 رد مع اقتباس
رد مع اقتباس